1 浮点计算问题

public class Oct2Bin {
    public static void main(String[] args) {
        double a = 0.1d;
        double b = 0.2d;
        System.out.println(a + b);
    }
}

结果为0.30000000000000004，而非0.3

2 小数计算丢精度原因

2.1 十进制小数转换为二进制小数方法

十进制小数转换成二进制小数采用”乘2取整，顺序排列”法。具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数 部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，或者达到所要求的精度为止。 然后把取出的整数部分按顺序排列起来，先取的整数作为二进制小数的高位有效位，后取的整数作为低位有效位。

2.2 、0.3背后丢精度的原因

0.3 x 2 = 0.6 ------取整数部分 0

0.6 x 2 = 1.2 ------取整数部分 1

0.2 x 2 = 0.4 ------取整数部分 0

0.4 x 2 = 0.8 ------取整数部分 0

0.8 x 2 = 1.6 ------取整数部分 1

0.6 x 2 = 1.2 ------取整数部分 1

0.2 x 2 = 0.4 ------取整数部分 0

0.4 x 2 = 0.8 ------取整数部分 0

0.8 x 2 = 1.6 ------取整数部分 1

……. 无限循环..........循环体1001

结果为 0.0110011001100110011001100………..

当然数据的存储长度肯定有有限的,所在最终变成了0.30000000000000004

3 Java中的float存储方式及计算方法

大家都了解int和float在Java中所占是4字节，但是int只能存储整数型，float是单精度浮点型，存储范围也比整数大，这是怎么产生的呢？

3.1 float的存储方式

首先，计算机不认识小数点，IEEE 754标准规定浮点数在计算机内存中是按照一个特定的方式来保存的(充分利用了每一bit)。见下图。

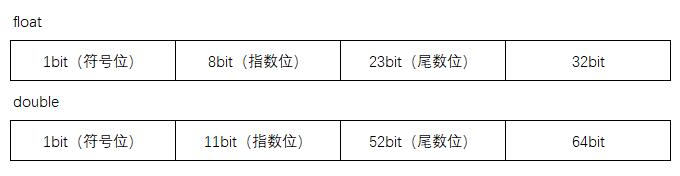
float在内存中共占32位，double共占64位，这也是单精度和双精度浮点数名称的由来。 在IEEE 754标准中，严格的表示形式是这样的：

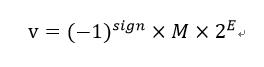
其中sign表示符号位，占一个字节, 0为正，1为负 E表示尾数位，M表示指数位 在float中sign占1bit，E占8bit，M占23bit， float能表示数据的最大范围是-2^128~2^128, 所以肯定比int类型大 double中sign占1bit，E占11bit，M占52bit，double能够表示的范围大，所以常常float叫单精度，double叫双精度。

3.2 举例论证数据存储

在十进制当中，一个数可以这样表示：

520 = 5.20 * 10 ^ (2)

那么同理，浮点数 float x = 8.25f 也可以这么表示，例如：

那么它的浮点表示方式为:

1000.01 = (-1)^0 * 1.00001 * 2 ^ (3)

对应到上面符号，sign 符号位是正数，在计算机中存储为0，1.00001表示M，在计算机中存储为100001，由于这里整数部分的1始终不变，所以可节约出来，这样M的精度范围就增加了一位。

指数部分3，对应符号E，在计算机中存储数字位 3+127 = 130，二进制码为10000010，这里我要着重说一下为何指数部分的表示为什么要加127 ？

因为阶数部分是8，但不包含首位符号位，所以对于计算机判断来说这8位就是个无符号整数，表示范围0～255，但是实际中我们的阶数部分是需要负数的，去掉全0表示负无穷，全1表示正无穷，所以剩下的部分就是1～254，为了公平各一半，所以要加上127，1～127的范围表示负数，例如E = -3，所以在计算机中表示为-3 + 127 = 124，当E = 3时，计算机中保存的是3 + 127 = 130，我想这么说应该很清楚了。

所以总结上面 8.25 在计算机中的存储值是
0 10000010 00000000000000000100001